cs231n-lec4

计算图

计算原理

图中的每个结点是计算的一个步骤，每个运算结点只管输入该结点的数和输出的计算结果

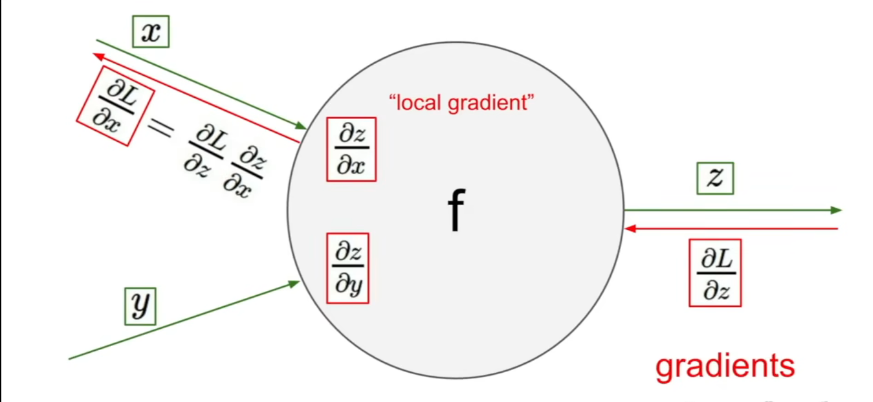
计算图结点

正向传播时，计算相对输入数的梯度，反向传播回来的时候，能通过链式法则计算处损失函数相对此处的梯度。所以只需要在每个结点处计算局部梯度

比如 $f(x,y,z)=(x+y)z$ ，计算梯度的过程是利用链式法则反向计算偏导数的过程

计算图

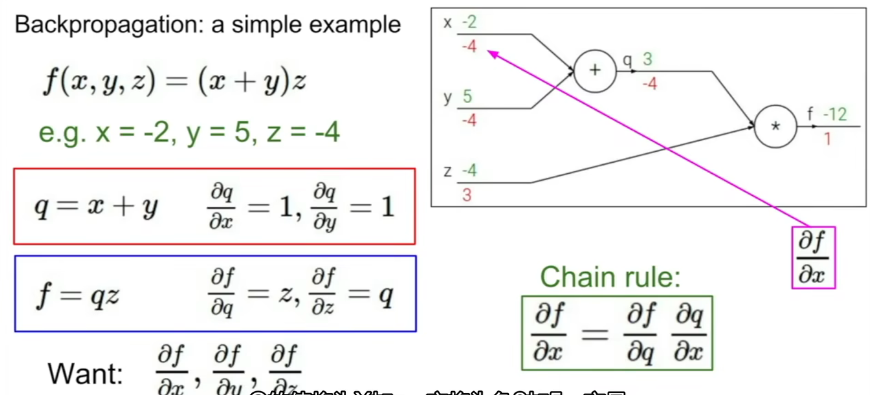
计算图结点的计算粒度可以通过我们自己定义，最简单的是每个结点只计算加法，乘法等运算的梯度，也可以定义更复杂函数的结点，比如 sigmoid 函数

$\sigma(x)=\frac{1}{1+e^{-x}} \\ \frac{\mathrm d\sigma(x)}{\mathrm dx}=(1-\sigma(x))\sigma(x)$

这是一个计算粒度和计算图复杂性的权衡

当输入是向量时，计算梯度要用 Jacobian 矩阵，详见自动梯度

模块设计

每个计算图都是要给模块，需要给模块设置前向传播计算输出以及反向传播计算本地梯度。比如乘法模块类似：

class MultiplyGate(object):
    def forward(x, y):  
        z = x * y
        self.x = x
        self.y = y
        return z
    def backward(dz):
        dx = dz * self.y
        dy = dz * self.x
        return [dx, dy]

深度学习框架